实验离心技术的基本计算法（三）

五、沉降系数的近似计算

（Ⅰ）利用速率一区带密度梯度离心作沉降系数的近似计算；
用超速（ 40000~42000转/分）细长离心管（ 10~13毫升，离心管长 9~10厘米）选用线性梯度或凸指数梯度（可以提高在较高密度区的分辨率）。

测定样品在相同的离心条件下（温度、转速、加减速速率，转头、离心管样品量，梯度材料及梯度曲线等等）以不同沉降时间离心数次，测出沉降带的位置（昀好用梯度仪抽出，经蠕动泵至带流动池的分光光度计检测某一纯样品带的位置，昀后用部分收集器收集）即可计算 S值。不同的离心时间（如 t₂,t₁），代入ω (角速度)，r为轴心至沉降面距离（厘米）、t为离心时间用分表示。
用移动界面法，分析用超速离心机或带分析附件的制备用超速离心机，从照相的纹影（schlieren）图上用比长仪测定（界面）的位置，以log r对t作图，可以求得直线斜率：

从中算出 S值。
如果 log r－t不是直线，则可以分别求每个时间的S值然后作s-t图，并外延至t=0时的S作为计算标准。当然，S也要化成 S_20.W。

（Ⅱ）某些生物大分子的沉降系数与分子量之间关系时经验公式：

六、转子常数：在计算沉降时间公式（12）中我们曾引入转子常数K（公式 13）。离心机说明书上绘出的 K值是指该转头在昀高转速时从r_min沉降到r_max时的K值。实际上我们一般不用N实际，而沉降也往往是从某初始位置rl沉降到终了位置 r2.
于是在这种情形中

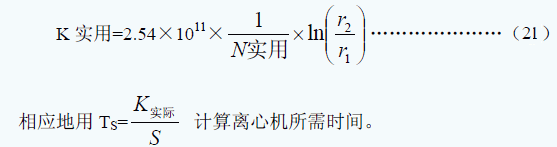
对于同类转头，K值越小，使用价值越高，在选择离心条件时有更大的余地。对不同类别的转头，由于它们的特点和用途不同，K值是衡量转头性能的一个因素。
由于转头在容量上的差异，使它们的综合利用价值不局限于K值。我们近可以引入另一个系数 L：

式中 V_R为转子各离心管名义容量的总和，用厘米³表示，同类转子的价值差异，除了材料加工等因素外还要取决于 L值，L越小，价值越高。
在欧洲还常常用Pi值来表达转子的性能

七、分子量计算：

已知沉降系数，可以用经验公式计算分子量，反之亦然［五节之（Ⅱ）］也可以用超离心法先求得沉降系数，扩散系数，再来计算分子量。
设在溶剂内悬浮的样品颗粒在离心场中有效质量为m，角速度ω，瞬时回转半径r , 沉降速度为υ，在粘性流体中匀速沉降的摩擦系数为 fo。
根据力学平衡原理：

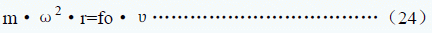
由于颗粒悬浮在溶液中设其真实质量为m_r ,σ为颗粒密度ρ为溶剂密度，于是有

参考文献：

[1] Fujita,H.“Mathematical theory of Sedimentation analysis” A cademic press.New York 1962

[2] Steensgaard.J等“Methodological developments in biochemistry”vol:4,P67,1974

[3] S.P.Spragg等“Theoretical aspects of practical centrifugation”IRL press. Oxford Uni.Press(1992)

[4] 余兴明“质粒 DNA的超速离心分离”生命的化学 vol:14 No:1 pp11~15 1994